PID calculations
CNT-APG002-EN 5
®
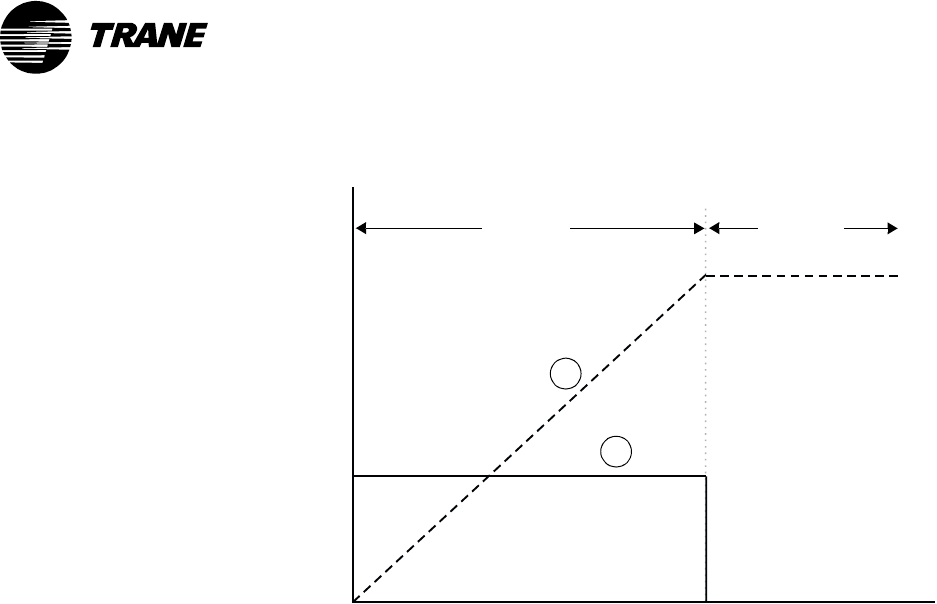
Figure 5: Integral output added to proportional output
The value of the integral calculation can build up over time (because it is
the sum of all past errors), and this built-up value must be overcome
before the system can change direction. This prevents the controller from
over-reacting to minor changes, but can potentially slow down the
response.
One drawback to integral control is the problem of integral windup. Inte-
gral windup occurs when the sum of the past errors is too great to over-
come. This can happen when the HVAC equipment does not have enough
power to reach the setpoint; the integral windup only increases as the
equipment struggles to reach the setpoint. To minimize the problem of
integral windup, Trane controllers use a method of PID control known as
the velocity model, which is described in “Velocity model” on page 7.
Derivative calculation
The derivative calculation responds to the change in error. In other
words, it responds to how quickly the measured variable is approaching
setpoint. The derivative calculation can be used to smooth an actuator
motion or cause an actuator to react faster.
However, derivative control has several disadvantages:
• It can react to noise in the input signal.
• Setting derivative control requires balancing between two extremes;
too much derivative gain and the system becomes unstable, too little
and the derivative gain has almost no effect.
• The lag in derivative control makes tuning difficult.
• Large error deadbands, common in HVAC applications, render deriv-
ative control ineffective.
Output
Time
Error ≠ 0
Error = 0
Proportional + integral
output
Proportional + integral
output when proportional
output has gone to zero
1
2
Proportional-only
output


















